

Then it finds the third smallest and swaps, then the fourth smallest and swaps, then the. What does our algorithm do after this first swap? It finds the second smallest entry in the array and swaps it into position 1. Swapping values like this is actually quite common - especially when sorting. This is done by using an extra variable to help with the swap. What if the smallest entry is in poition "i" in the array? The algorithm swaps the value in position i with the value in position 0.

For sorting in increasing order, this element should be in position "0" in the array. It starts by looking for the smallest element in the array. Using this "key and satellite data" method we can use these same sorting algorithms on almost anything.įirst, here's some example code for Selection Sort. Along with the key values I would also need to update the satellite date that goes along with it: the customer's names. However, just sorting those keys isn't helpful by itself. Those with smaller "keys" would be seated first. The numbers I'm sorting could be random numbers given to customers waiting to be seated at a restaurant. Last thing: the entries that we're sorting could also be thought of as keys representing lots of other data. Remember that for objects we would have our objects implement the Comparable interface and define the compareTo method. Any other primitive type or object that can be compared could be used just as well. In the implementation of each algorithm below it is only sorting an array of integers. But how do we get that array sorted in the first place? Today we'll introduce 3 basic algorithms for sorting an array of elements: Selection Sort, Insertion Sort, and Bubble Sort. Binary Search relied on it's input array already being sorted.
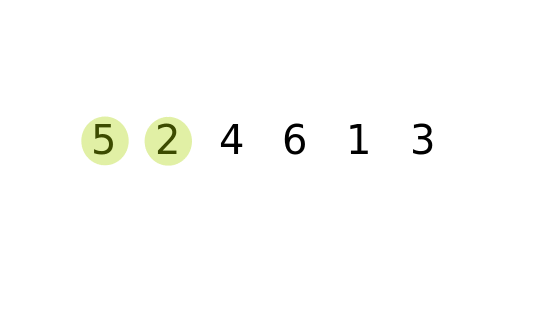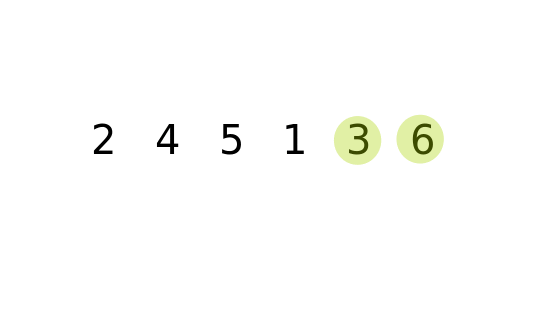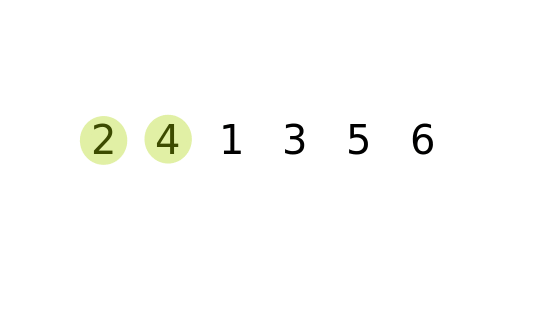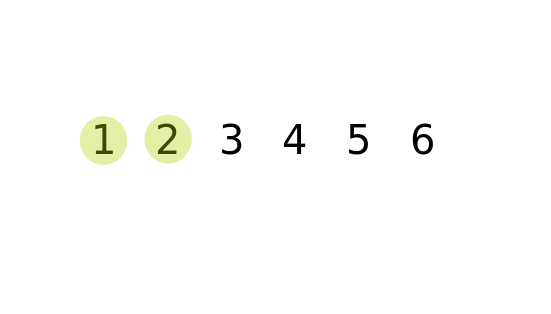
In the last lecture we compared two searching techniques: Linear Search and Binary Search. There’s a simplification we can apply: the steps ofįinding the proper sorted position and inserting/shifting it there can beĬombined into a single loop.CS 1 : Lecture 21 Lecture 21: Sorting Algorithms This is an array/vector, inserting an element requires shifting all the elementsĪfter it up one step. We insert it into the sorted section, in its proper, sorted, position. For each element in the unsorted section, Suppose we split the input into two “sections”, sorted and unsorted. Template int binary_search ( const vector & data, const T & target, int low = 0, int high = data.


 0 kommentar(er)
0 kommentar(er)
